「青空文庫、縦書きで読みてぇ〜」→Kindle 版ありました
タイトルのとおりです。
青空文庫にはKindle版が存在します。
もちろん無料です。
こんな感じです(画像)
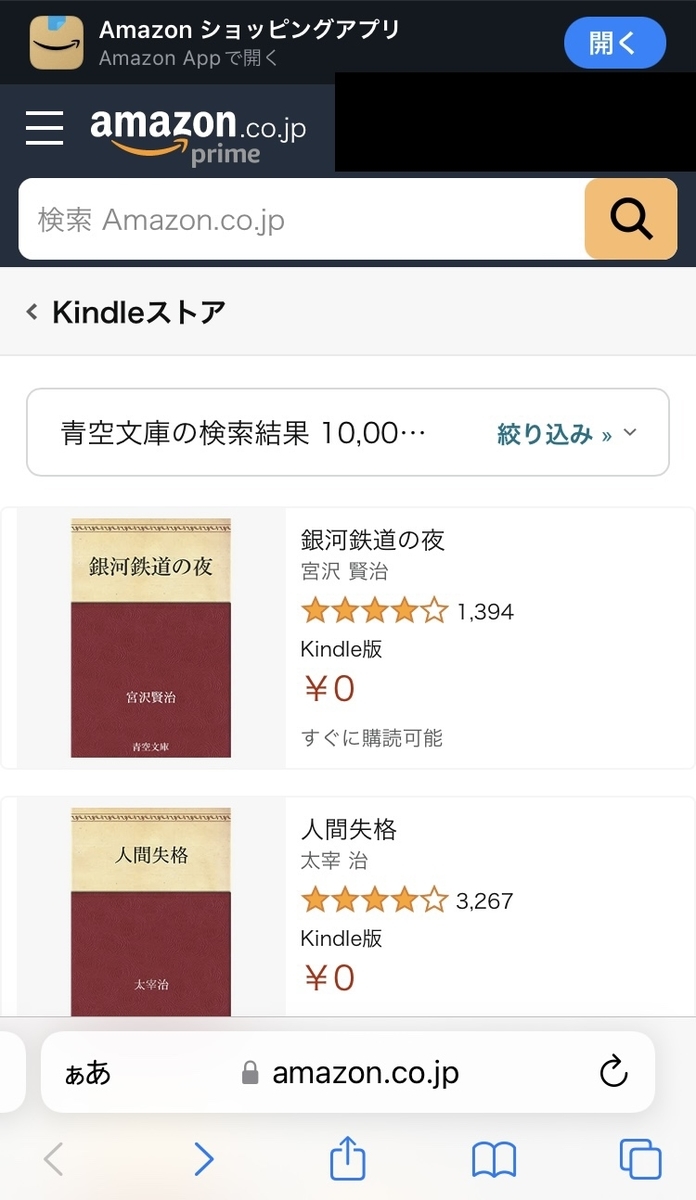
表紙はどの作品も共通で、上部はくすんだ感じのベージュ背景と黒文字タイトル、下部は深め渋めの赤色背景に白文字で作者名、最下部に青空文庫と書かれています。
縦書き、なんて素晴らしい響き…。
あとルビも付いています。最高か。
実際にやってみた。
iosやandroidでKindleアプリを使って青空文庫を読みたい場合、safariやchromeなどのブラウザアプリで作品を「購入」する必要があります。
青空文庫のKindle版は無料なんですが、Kindle的には「0円の本を買う」という扱いなんですね。
Kindle Unlimited や Prime リーディングの対象作品なら、Kindleアプリ上で「利用を開始する」みたいなボタンをポチるだけなんですけどね。
青空文庫はこれらの対象には入っていないので仕方ありません。
以下は iPhone での手順です。

まずは safari か chrome か、とにかくブラウザアプリから Kindle ストアにアクセスします。
www.amazon.co.jp
上の画像では単に「青空文庫」という言葉で検索していますが、実際には読みたい作家や作品の名前のあとに青空文庫と付けて検索する場合が多いと思います。
試しに「銀河鉄道の夜 青空文庫」と検索してみると、トップに青空文庫版の銀河鉄道の夜が表示されました。
続いて、個別の商品ページに飛びます。

はい、0円ですね。
Kindle版を選択した状態で「今すぐ無料で取得」をタップします。

これで入手完了です。
続いてKindleアプリを開きます。
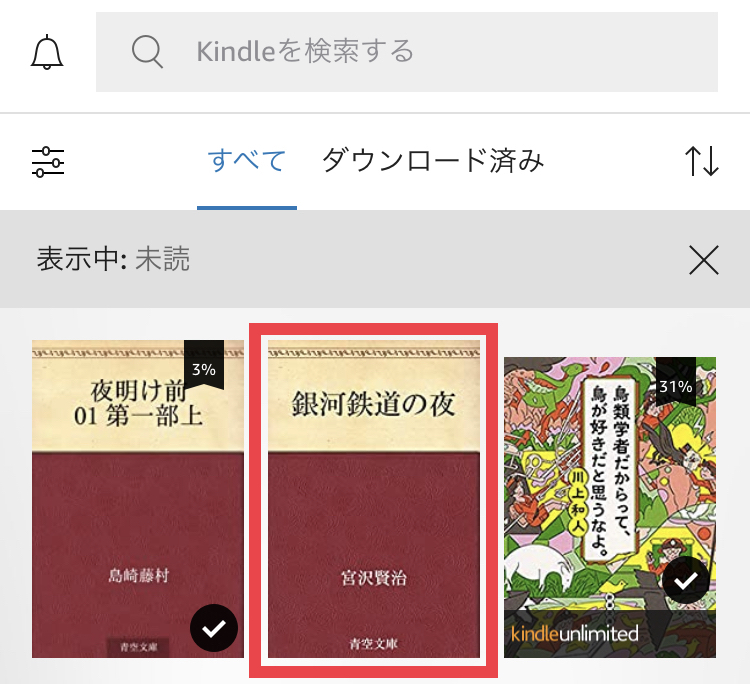
先ほどKindleストアで取得した銀河鉄道の夜がライブラリに追加されています。
あとは作品をタップしてダウンロードすれば読み始められます。
お疲れさまでした。
PostgreSQL から MariaDB(MySQL)へのマイグレで知っておきたかった事
DBの移行なんて二度とやりたくねンだわ。
redmineのDBをPostgreSQL から MariaDB(MySQL)に切り替えたときいろいろ調べたので供養。
DB間の違い
文字コード - MariaDBにテーブルを作る前に知っておきたいこと
MySQL系で言う utf8 は utf8 じゃない。
何を言ってるかわからないだろう。
つまりこれを読めということです。
じゃあ実際どうすんのよという話はこれらを読むとよい。
一応ドキュメントも載せておくが、何を言っているのかよくわかっていない。
文字列の扱い - dumpファイルの修正時に知っておきたいこと①
PostgreSQLとMariaDBはどちらも、文字列を扱う場合に使えるデータ型としてvarcharとかtextとかがある。
しかしPostgreSQLとMariaDBでは、同じtext型でも性質が異なるので注意されたい。
具体的な話は以下の記事が詳しい。
また、公式のドキュメントも確認しておくとよろしい。
英語読むのがだるい人はdeeplでも使ってください。
過去記事でdeeplのchrome拡張の導入と使い方の紹介してます。
MySQLでのvarchar型についてもっと深堀りしている方もいました。
連番を付ける - dumpファイルの修正時に知っておきたいこと②
- PostgreSQLではSEQUENCE/MariaDBではAUTO_INCREMENT
- と言いつつも、MariaDBでもSEQUENCEは使える(らしい)
- AUTO_INCREMENTは…
- 主キーかユニークキーが設定されたカラムにしか使えない
- データ型は整数か浮動小数点数。text型はNG
- 1つのテーブルに対して1つだけ指定できる(しなくてもいい)
PostgreSQLとMariaDBでは連番の付け方が異なる。
以下の記事では MySQL と PostgreSQL で連番の設定をするならそれぞれこんな感じになるよねということが書いてある(2012年の記事のため参考程度に)
ただ、MariaDB 10.0以降はSEQUENCEが使えるようになったらしく、PostgreSQLと同じような使い方ができるのかもしれない(未検証)
ちなみにPerconaだとシーケンスは使えない。
以下はそれぞれどんな感じで使うのか調べたもの。
一応、有償ソフトもある
いろいろリンクを貼ったが、有償ソフトを使って変換してしまう方法もある。
一例としてDBConvertというソフトがある。
これについてはeasyredmine(redmineの有償拡張パッケージ)の開発元がPostgreSQLからMySQLの移行に良いよ!と太鼓判を押している。
しかし値段が10万円を超えるため、個人で買うのは厳しいところ。
PostgreSQL 小ネタ
SQL構文
ドラム式洗濯機は設置業者によって置けたり置けなかったりする造
先日ドラム式洗濯機を手に入れました。
ドラム式洗濯機最高です。
でも設置までにすったもんだありました。
1回目の設置前調査では業者に「お住いのお部屋だとドラム式洗濯機自体置けませんね」と不可判定をもらってたんです。
後日別の家電量販店に行ったらふつうに設置してくれました。
この記事の主旨は、
「設置業者によって置ける・置けないの基準は違う。諦めんなよ…諦めんなよ、お前!!どうしてそこでやめるんだ、そこで!!もう少し頑張ってみろよ!(以下略)」
です。
設置業者さん「ドラム式洗濯機は諦めてください」
最初はBックカメラで購入しました。
選んだのはSHARP製のドラム式洗濯機のなかでいちばん小さいやつ。
蛇口の高さは心配でしたが、そのほかのポイント(搬入経路、防水パンのサイズ、防水パン周辺の空間的な余裕など)は大丈夫そうだし、まあいけるだろうと。
いざとなったら蛇口だけ壁ピタに交換すりゃいけるいける!と高を括っていました。
Bックカメラの提携業者さんに設置前の現地調査(無料)に来てもらったのですが、こちらの先人様が書かれた記事とほとんど同じ流れの会話になりました。
業者さんの話をまとめると、「蛇口の高さ、横幅、奥行き全部アウト!ドラム式洗濯機自体置けないよ!」とのことでした。
諦めが悪いので改めて自分で洗濯機周りの寸法やカタログなどを調べ直しました。
そしたらやっぱり蛇口の高さは心配でしたが、そのほかのポイント(搬入経路、防水パンのサイズ、防水パン周辺の空間的な余裕)は大丈夫だし、まあいけるだろうと。
いざとなったら蛇口だけ壁ピタに交換すりゃいけるいける!と高を括り直しました。
で、蛇口交換するからもう一回現地調査来てくださいよ~とお店にお願いしたんですが、横幅や奥行きでNG判定が出てる以上意味ないですよ~と言われちゃいました。まあそれはそう。
設置業者さん「ドラム式洗濯機置けますよ~」
やっぱり諦めが悪いので、お店を変えることにしました。
お次はYマダ電機です。
在庫の関係で日立のビックドラムにしました。
二回目の設置前調査(無料)。
設置業者さんはBックカメラに依頼したときとはもちろん別です。
設置業者さん「あーちょっと(蛇口までの)高さが足りないかなぁ…」
とのことだったので、「蛇口は壁ピタ水栓に替える予定です!!!!!」と食い気味にお伝えしました。
設置業者さん「あ、それなら置けますよ~」

設置業者の方はあくまで現在の設備状況で置けるか置けないかを見ているっぽいので、こういうことは自分から言っていかなきゃですね。
設置当日もこれといった問題はなく、無事にドラム式洗濯機を設置することができました。
ありがとうございます、ありがとうございます。
補足:壁ピタ水栓の交換工事について
しれっと書きましたが、ドラム式洗濯機を置くために蛇口を壁ピタ水栓に替えました。
壁ピタ水栓 CB-L6 商品概要 | 洗濯機/衣類乾燥機 | Panasonic
壁ピタ水栓は本体を固定するために留め具を取り付けるため、壁に穴が開くことになります。
賃貸に住んでいる場合は、管理会社か大家さんに交換工事をしてもいいか、壁に穴を開けることも含めて事前に確認しておきましょう。
ちなみにビックカメラで買うと交換工事(有料)の手配もしてくれます。
手配の都合上、工事は早くても3,4日くらい先になるとのことで、実際自分がお願いした時もそれくらいだったような気がします。
ヤマダ電機では壁ピタ水栓の設置工事の手配はしていないっぽいです(ヤマダ電機の店員さんに聞いた)
他の家電量販店については知らん。ご自身でお店までお問い合わせください。
3日も待ってられねンだわという人は交換工事の業者を調べて依頼するか、自力でやるかになると思います。
自分の住んでいるエリアでは、見積もり的には壁ピタ水栓の工事で検索していちばん上に出てくる会社(くらしのマーケットではないです)よりBックカメラに頼んだほうが壁ピタ本体料金込みで安い感じでした。
この辺りの話は地域差もあると思うのでご自身でググってください。
交換工事から1週間経たないうちに水漏れしたからモンキーレンチ買って自分で絞ったのは内緒。
まとめ:だからこそ Never give up!
業者によって設置可否の基準違うかもしれないから、一回設置無理って言われても諦めんなよ!というお話でした。
そのためにも、自分から測定や情報収集をやっていきましょう。
Yマダ電機の設置業者さんも、こちらが壁ピタ水栓の話をしなければ「蛇口の高さが低いので置けません。さよなら~」となってたかもしれませんし。
なんやかんや設置まで大変でしたが、ドラム式洗濯機があまりにも便利なのですべてを許しました。
最後に、この記事では家電量販店の名前をほぼ出しちゃってますが、全国どこでも同じような状況が当てはまるって話ではありません。サンプル数1です。
地域によってはBックカメラの設置業者さんは置けるって言ったけどYマダ電機の設置業者は置けないって言っていた、とか、もしかしたら同じ店舗でもどの提携業者さんが対応するかによって置ける・置けないが変わったりとかあるかもしれません(ヨドバシとか他の系列店は今回行ってないから知りません)
繰り返しになりますが、細かい話はご自身で調べてみてください。
だからこそ Never give up!
【朝はパン】食パンをレンジで解凍する最適解を見つけました【パンパパン】
以下の条件に対して、
- 6枚切りの食パン1枚(冷凍済、サランラップで包んだ状態)を、
- 600ワットの電子レンジで、
30秒加熱→裏返して20秒
これです。
冷凍した食パンを電子レンジで温めるときの加減って地味に難しくないですか?
(簡単だぞという自炊強者はお引き取りください)
加熱しすぎると片側だけ水気のあるフニャフニャな感じになるし。
かといって短時間にすると解凍が不十分で何回も温めなおすことになって面倒だし。
そういうわけでいろいろ試した結果、はじめに書いた手順がいちばん良い感じでした。
食パンの厚み(何枚切りか)やレンジのワット数によって調整は必要ですが、参考にしていただければ。
疲れた社会人に送る「独身サラリーマン鈴木の生態」
全ての疲れた社会人の心を揺さぶる名作、「独身サラリーマン鈴木の生態」について。
先に断っておくが、この作品は主人公が特別な才能で成り上がるとか、大きな目標を成し遂げるとか、そういったドラマチックなものではない。
むしろ、ごくごくありふれた悩みを抱える社会人の物語である。
続きを読むはじめてのDeepL公式Chrome拡張機能
アフロは最強のソリューションである

さいきん、久々に友人数名で飲み会にコミットしました。
皆良い奴らなのですが、毎回誰かしら遅刻するのが玉に瑕です。
せっかく久々に会うわけですし、少しでも長く彼らと過ごしたいなと思い、いちばん遅かった人には罰ゲームを与えます!と予め宣言しておきました。
当日、いちばん遅かったのはぼくでした。
続きを読む【一人暮らし】アパートにドコモ光を新規で開通するまでの備忘録
先日、家に新規でドコモ光を開通しました。
それまでにちょっとトラップがあったのでそのことを記録しておきます。


![Nintendo Switch 大乱闘スマッシュブラザーズ SPECIALセット[同梱ダウンロード版ソフト引換期限:2019年4月15日まで] Nintendo Switch 大乱闘スマッシュブラザーズ SPECIALセット[同梱ダウンロード版ソフト引換期限:2019年4月15日まで]](https://m.media-amazon.com/images/I/41XcWZkJD9L._SL500_.jpg)