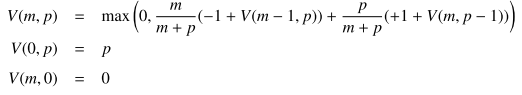NEW GAME!を観ました。プログラミング始めます。(24)
Fate/stay night [Heaven's Feel] I.presage flower 面白かったです。

※基本的に、愛知大学の有澤先生がプログラミングの講義で使用しているテキスト「Pythonによるプログラミング入門」に沿って進めています。
※Python 2.7.13を使用しています。
今回のテーマは「Boyce の壷の問題」です。第 I 部 Python 入門最後の内容です。
Boyce の壷の問題
1. 問題の提起
壷が1つあります。中には白の碁石が4個、黒の碁石が6個入っています。
- この壷から石を1つずつ取り出します。
- 一度取り出した石は壷に戻すことができません。
- 白い石を引いた場合には100円もらえます。
- 黒い石を引いた場合には100円支払わなければいけません。
- 壷から石を取り出すのは途中でやめてもOKです。
さて、このゲームは参加することでどのくらいの利益が期待されるのでしょうか?
これが今回のテーマである「Boyce の壷の問題」です。ただし、問題にあるように、白石と黒石の数がわかっていることを前提としています。
高校の時に習った期待値の計算を思い出しますね。「途中でやめてもOK」ということなので、感覚的には参加するのは全然アリだと思いました。
2. プログラムの考え方
細かいことはテキストを見ていただくとして、まずはプログラムを見て全貌を見てみましょう。
譜 4.15 Boyce の壷の問題を解くプログラム
def V(m,p): if m==0: return p if p==0: return 0 return max(0, float(m)*(-1+V(m-1,p))/(m+p)+float(p)*(1+V(m,p-1))/(m+p)) # results are always >=0 because of max(0, V) for p in range(0,10): print p, for m in range(0,10): print "%5.2f"%V(m,p), # "%5.2f" means xxx.xx data print # About result table # 1st column shows p (numbers of white stone) # 2nd column shows the benefit when m=0 (numbers of black stone) # 3rd column shows when m=1, 4th shows when m=2, ...引用元:Pythonによるプログラミング入門, p. 58(コメントアウトはK介による。)
結果
0 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 1 1.00 0.50 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 2 2.00 1.33 0.67 0.20 0.00 0.00 0.00 0.00 0.00 0.00 3 3.00 2.25 1.50 0.85 0.34 0.00 0.00 0.00 0.00 0.00 4 4.00 3.20 2.40 1.66 1.00 0.44 0.07 0.00 0.00 0.00 5 5.00 4.17 3.33 2.54 1.79 1.12 0.55 0.15 0.00 0.00 6 6.00 5.14 4.29 3.45 2.66 1.91 1.23 0.66 0.23 0.00 7 7.00 6.12 5.25 4.39 3.56 2.76 2.01 1.34 0.75 0.30 8 8.00 7.11 6.22 5.35 4.49 3.66 2.86 2.11 1.43 0.84 9 9.00 8.10 7.20 6.31 5.43 4.58 3.75 2.95 2.21 1.52
1~5行目 def V(m, p):
今回のプログラムの肝です。黒石がm個、白石がp個の場合に期待される利益V(以下、期待利益と呼びます)を計算してくれます。たとえば、V=1.4 であれば140円となります。
(引用元:Pythonによるプログラミング入門, p. 58)
Vの計算式は上記のように考えられます。式の詳細はテキストを参照していただくとして、ここではざっくりとした説明にとどめます(でも長いです)。
まず一つ目の式は max(0, ...) という形になっています。これは「0と...を比較して、値の大きい方を採用する」という意味で、出力される結果を0以上にするための措置です。期待利益が0を下回る場合には参加する価値がないので、具体的な値を知る必要はありません。
max()内の右側の式について。
1つ目の項は、以下のような意味を持っています。
(黒石を引く確率)×{(黒石を引いたときの期待利益)+(黒石を引いた後、壷に残る石から予想される期待利益)}
また、2つ目の項は上記の黒石が白石になった場合です。
いま、「黒石を引いた後、壷に残る石から予想される期待利益」は条件式である V(0, p) = p と V(m, 0) = 0 から計算できます。1つ目は壷に白石しかない場合の期待利益、2つ目は壷に黒石しかない場合の期待利益です。壷に白石しかないなら全部引けばそのまま利益(p)になりますが、全部黒石であればそれ以上引く意味はありません(0)。
テキストで紹介されている m = 6, p = 4 の場合を考えると、(黒石を引いた後、壷に残る石から予想される期待利益)= V(m-1, p) = V(5, 4) というのは条件式が当てはまらないため直接に計算できません。そこでプログラムにあるように、再帰的に考えます。すると、そのうち V(0, p) や V(m, 0) が表れ、それが return されることでなんやかんや計算が出来ます。
この辺りの解釈は言葉を並べられてもよくわからないと思うかもしれません。
プログラムが得意な先輩によると、再帰的な計算は自分で紙に書いて流れを追ってみるとわかりやすいそうです。
私も前回の置き石ゲームのプログラムを読むにやってみましたが、書き出すことで頭の中が整理されて理解の助けになりました。
7~10 for p in range(0,10):
白石の数 p=0~9 の場合それぞれについて、p の値と (白石, 黒石) = (p, m) のときの期待利益V を表示します。ただし、それぞれの p について m=0~9 を試しています。
結果の見方に関する説明は下記の通りです。
左端の列の数字は p を表している。その右の列は m=0 の列である。そして順に m=1, m=2 の列が続く。従って、例えば 3 行目、3 列目の 1 . 33 は V(2 , 1) の値である。この表から V(6 , 4) は 0 . 07 であることが分る。つまり黒石 6 個、白石 4 個でもゲームに参加する価値があるのである。
(引用元:Pythonによるプログラミング入門, p. 58)
というわけで、黒石の数が白石よりも多いからといって、必ずしも期待利益が0を下回るとは限らないということがわかりました。
3. 譜 4.15 の改良
さて、譜4.15 によって計算結果を得ることはできましたが、このプログラムには大きな問題があります。
それは、計算にとても時間がかかることです。この原因についてもテキストで述べられています。
理由はひどく無駄な計算をしているからである。例えば V(3 , 5) の計算をする時には V(2 , 5) の計算が行われている。V(2 , 6) の計算を行う時にも V(2 , 5) の計算が行われている。すでに計算済の結果を使用しようとはしていないのである。
(引用元:Pythonによるプログラミング入門, p. 58)
これを解決する改良版として紹介されるのが譜 4.16 です。
譜 4.16 譜 4.15 の改良版
u={} # empty library def V(m,p): if m==0: return p if p==0: return 0 if (m,p) in u : return u[m,p] r=max(0, float(m)*(-1+V(m-1,p))/(m+p)+float(p)*(1+V(m,p-1))/(m+p)) u[m,p]=r return r for p in range(0,10): print p, for m in range(0,10): print "%5.2f"%V(m,p), print(引用元:Pythonによるプログラミング入門, p. 59)
改良に当たっての重要なポイントは1, 5, 8行目です。
1行目 u={}
u という空の辞書を定義します。8行目でこれに V の計算結果を保存します。
前回の置き石ゲームで使用したのは d = [] でしたが、これはリストです。今回のように辞書を作成する場合には {} を使います。使い分けに注意ですね。
5 if (m,p) in u : return u[m,p]
もしも (m, p) の組み合わせがこれまでに計算したものの中にあれば、それを利用しますよ、という意味です。これによって同じ計算を繰り返すことがなくなり、大幅に計算が短縮されます。
8 u[m,p]=r
直前の6, 7 行目で計算している r (= 期待利益V) をそのときの (m, p) と関連付けて辞書に保存します。
これらの加筆・修正によって、結果は譜 4.15 と同じですが計算時間を大幅に短くすることができます。是非ご自身で両方試してその速さを感じてほしいです。
最後に、この節の最後に筆者が述べていることを引用させていただき、締めの言葉としたいと思います。
プログラムを作る時には、まずは堅実なプログラムを作成するがよい。誤りがないと言う事が最も大切である。実行速度を上げるためにプログラムを工夫すればするほど誤りが持ち込まれる可能性が高くなる。工夫したプログラムは堅実なプログラムと実行結果を比較する事によって誤りを回避する事が可能である。
(引用元:Pythonによるプログラミング入門, p. 59)