NEW GAME!を観ました。プログラミング始めます。（15）

11話のねねっちは一段と最高でしたね！
f:id:kirintt:20170928205657p:plain

※基本的に、愛知大学の有澤先生がプログラミングの講義で使用しているテキスト「Pythonによるプログラミング入門」に沿って進めています。
※Python 2.7.13を使用しています。

今日のキーワード
- 1752 年 9 月
  - 問１
感想

今日のキーワード

1752 年 9 月

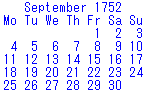
ところで実は Python には calendar モジュールが備わっており、cal(y,m) に相当する関数 prmonth(y,m) が存在する。これを使って 1752 年 9 月のカレンダーを表示させると…
（引用元：Pythonによるプログラミング入門, p.35）

ﾅﾝﾀﾞｯﾃｰ！
早速やってみよう。

from calendar import * 
prmonth(1752, 9)

結果
f:id:kirintt:20170928202716p:plain

会話モードでの練習でも登場していたが、

from 〇〇 import *  # 〇〇はモジュール名

と書くことで、特定のモジュールの関数を使うことができる。
また、ここでの"*"は全てを意味している。特定の関数のみを使いたいときは、

from 〇〇 import △△  # △△は関数名

と書いてもOK。

ちなみにUNIXのcalコマンドで1752年10月を表示すると上の図とは異なる結果になるらしいが、これはイギリスの暦の歴史を考慮しているためらしい。

問１

グレゴリオ暦の前にはユリウス暦が使用されていた。ユリウス暦では単に 4 で割り切れる年を閏年と定めた。(つまり 1 年間を 365.25 日と考えたのである。) ユリウス暦は 1582 年10 月 4 日 (木曜日) を最後にグレゴリオ暦に改められその翌日が 10 月 15 日 (金曜日) と定められた。従って Zeller の公式はユリウス暦の下では次の様に修正される。
def h0(y,m,d):
    if m<3: y=y-1; m=m+12
    return (y+y/4+(13*m-2)/5+d)%7
この下で 1582 年 9 月のカレンダーを表示しなさい。また、ユリウス暦とグレゴリオ暦が接続された 1582 年 10 月のカレンダーを表示しなさい。(ヒント: 接合月を表示する関数を柔軟にしてシンプルに設計すること。)

まず1582年9月のカレンダーをユリウス暦で表示。

# coding: shift-jis
    # 日本語使います宣言
#def h(y,m,d):
#    if m<3: y=y-1; m=m+12
#    return (y+y/4-y/100+y/400+(13*m+8)/5+d)%7

def h0(y,m,d):
    # hは今回使用しないのでコメントアウト（上）
    if m<3: y=y-1; m=m+12
    return (y+y/4+(13*m-2)/5+d)%7

def cal0(n,m):
    for x in ("sun","mon","tue","wed","thu","fri","sat"): print " ",x,
    print
    for x in range(0, n): print "  ---",
    for x in range(1, m+1):
        print "%5d"%x,
        if (x+n)%7==0 : print
    print

def cal(y,m):
    # y: year, 0,1,2,..
    # m: month, 1,2,..,12
    n=h0(y,m,1) # hをh0へ変更
    n1=h0(y,m+1,1)  # hをh0へ変更
    r=(n1-n)%7
    d=28+r
    cal0(n,d)

cal(1582,9)

結果
f:id:kirintt:20170928204042p:plain

前回知ったZellerの公式を使ったカレンダープログラム（譜3.10）を基に作成。

続いて、ユリウス暦とグレゴリオ暦が接続された月のカレンダーを表示。

# coding: shift-jis

# グレゴリオ暦(from 1582/10)
def h(y,m,d):
    if m<3: y=y-1; m=m+12
    return (y+y/4-y/100+y/400+(13*m+8)/5+d)%7

# ユリウス暦(to 1582/10)
def h0(y,m,d):
    if m<3: y=y-1; m=m+12
    return (y+y/4+(13*m-2)/5+d)%7

def cal0(n0,n,m):
    # n0: ユリウス暦におけるある月の最初の曜日
    # n: グレゴリオ暦におけるある月の最初の曜日
    for x in ("sun","mon","tue","wed","thu","fri","sat"): print " ",x,
    print
    for x in range(0, n0): print "  ---",
    for x in range(1, 5):
        print "%5d"%x,
        if (x+n0)%7==0 : print
    for x in range(15, m+1):
        print "%5d"%x,
        if (x+n)%7==0 : print
    print

def cal(y,m):
    # y: year, 0,1,2,..
    # m: month, 1,2,..,12
    
    # ユリウス暦
    n0=h0(y,m,1)    
    # n01=h0(y,m+1,1)  
    # r0=(n01-n0)%7
    # d0=28+r0

    # グレゴリオ暦
    n=h(y,m,1)      
    n1=h(y,m+1,1)  
    r=(n1-n)%7
    d=28+r

    cal0(n0,n,d)
    

cal(1582,10)