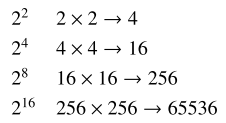NEW GAME!を観ました。プログラミング始めます。（22）

記事を書くとき、はてな記法にするのいっつも忘れてしまう。
f:id:kirintt:20171109214001p:plain

※基本的に、愛知大学の有澤先生がプログラミングの講義で使用しているテキスト「Pythonによるプログラミング入門」に沿って進めています。
※Python 2.7.13を使用しています。

今回のテーマは「再帰的アルゴリズム」です。

再帰的アルゴリズム
- おまけ

再帰的アルゴリズム

ここでは再帰的アルゴリズムがどれほど有り難いかを示そう。具体的なテーマとして第 4.3節に出て来た問題、すなわち、非常に大きな m に対して x ** (m − 1) を m で割った余りを計算する問題を取り扱う。
（引用元：Pythonによるプログラミング入門, p. 50）

テキストでは、例として x = 117, m = 1644455544992686074722684291497 について考える。
まず思いつくのは下記のようなプログラムだと思う。

x=117
m=1644455544992686074722684291497
print x**(m-1) % m
（引用元：Pythonによるプログラミング入門, p. 50）

でもやってみると全然結果が出ない…。
このほかにも、テキストではいくつか例が示されているが、どれもできない。
このような問題を解くには、そもそも発想を変える必要があるらしい。

　電卓を持っているとしたまえ。その下で 2 ** 16 の計算を考えてみよう。何回の掛け算が必要か? 15 回と答えると失格だ。次のようにたったの 4 回で計算できる。必要な計算量の差は m が大きい場合には凄まじい。

　こんなにうまく行くのは m が特殊な数だけか? そんなことはない。例えば m = 17 の場合には 2 ** 16 × 2 で計算できる。
（引用元：Pythonによるプログラミング入門, p. 51, 52）

天才かよ…。
これをプログラムで表現すると、以下のようになるらしい。

def pow(x,n):
    if n==0:
        return 1
    k=n/2
    y=pow(x,k)
    if n%2 == 0:
        return y*y
    return y*y*x

（引用元：Pythonによるプログラミング入門, p. 52）

pow(x, n) は x ** n を計算してくれるとのこと。
以下の様に考えることで、べき乗の計算が半分に！
n が偶数の場合：n = 2k として、x ** n を (x ** k) ** 2 として計算。
n が奇数の場合：n = 2k + 1 として、x ** n を x * (x ** k) ** 2 として計算。

関数 pow のように、その定義の内部に同じ関数を含む時に「再帰的関数」と言う。再帰的に計算法が表現されている場合に「再帰的アルゴリズム」と言う。
（引用元：Pythonによるプログラミング入門, p. 52）

この再帰的関数を使うと、例題は次のプログラムで計算できる。

譜 4.13 x ** (m − 1) を m で割った余りを計算するプログラム
def mpow(x,n,m):
    if n==0:
        return 1
    k=n/2
    y=mpow(x,k,m)
    if n%2 == 0:
        return y*y%m
    return y*y*x%m
m= 1644455544992686074722684291497
x=117
print mpow(x,m-1,m)
（引用元：Pythonによるプログラミング入門, p. 52）

結果

448225599079959033691973915232

すぐ計算終わった！すごぉい…。

おまけ

譜4.13 の pow(x,n,m) はもともと Python に入ってる関数らしい。
やってみた。

プログラム（１）pow

m= 1644455544992686074722684291497
x=117
print pow(x,m-1,m)

結果：譜4.13 と同じ

またしても一瞬で出たぁ。Python すげーな。
ついでに一つ発見があったのでメモ。
下記のプログラムだと実行できない。

プログラム（２）math モジュールの pow

from math import * 
m= 1644455544992686074722684291497
x=117
print pow(x,m-1,m)

結果

Traceback (most recent call last):
  File "(略)\mpow.py", line 4, in <module>
    print pow(x,m-1,m)
TypeError: pow expected 2 arguments, got 3

math モジュール内の関数 pow では pow(x, y) の計算しかできないらしい。pow(x, y, z) の形で使いたいときには math モジュールと区別する必要がありそう。

参考
2. 組み込み関数 — Python 2.7.18 ドキュメント
 9.2. math --- 数学関数 — Python 2.7.18 ドキュメント

今回はここまで！

次：まだ